[ad_1]

Researchers have made a big advance in spectral geometry by proving a particular case of Pólya’s conjecture associated to the eigenvalues of a disk. Their work, mixing theoretical class with potential sensible purposes, highlights the common worth and inventive fantastic thing about mathematical analysis. Credit score: SciTechDaily.com
A professor and his collaborators have confirmed Pólya’s conjecture for the eigenvalues of a disk, a tough downside in arithmetic.
Is it doable to infer the form of a drum from the sounds it makes?
That is the sort of query that Iosif Polterovich, a professor within the Division of Arithmetic and Statistics at Université de Montréal, likes to ask. Polterovich makes use of spectral geometry, a department of arithmetic, to know bodily phenomena involving wave propagation.
Breakthrough in Mathematical Conjecture
Final summer season, Polterovich and his worldwide collaborators—Nikolay Filonov, Michael Levitin, and David Sher—proved a particular case of a well-known conjecture in spectral geometry formulated in 1954 by the eminent Hungarian-American mathematician George Pólya.
The conjecture bears on the estimation of the frequencies of a spherical drum or, in mathematical phrases, the eigenvalues of a disk.
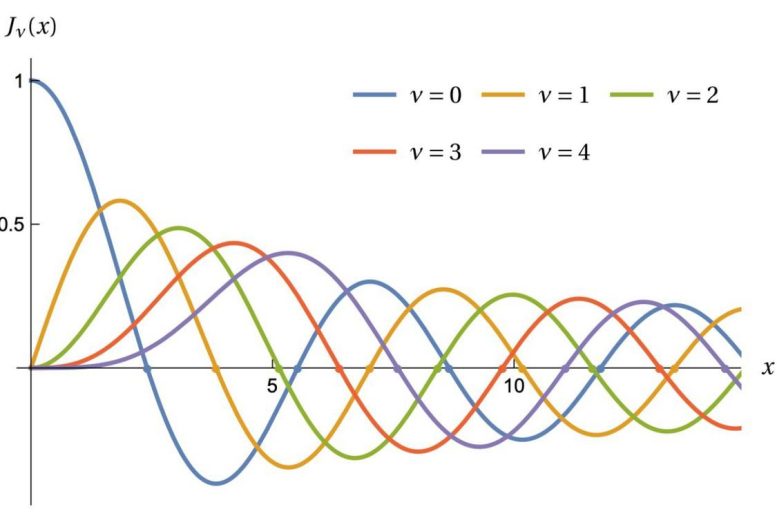
This graph reveals Bessel features, the place the factors correspond to the frequencies of sounds from a spherical drum. Credit score: Michael Levitin
Pólya himself confirmed his conjecture in 1961 for domains that tile a airplane, corresponding to triangles and rectangles. Till final 12 months, the conjecture was identified just for these circumstances. The disk, regardless of its obvious simplicity, remained elusive.
“Think about an infinite ground lined with tiles of the identical form that match collectively to fill the area,” Polterovich mentioned. “It may be tiled with squares or triangles, however not with disks. A disk is definitely not a good condition for tiling.”
The Universality and Influence of Arithmetic
In an article revealed in July 2023 within the mathematical journal Inventiones Mathematicae, the researchers present that Pólya’s conjecture is true for the disk, a case thought of notably difficult.
Although their result’s basically of theoretical worth, their proof technique has purposes in computational arithmetic and numerical computation. The authors are actually investigating this avenue.
“Whereas arithmetic is a basic science, it’s much like sports activities and the humanities in some methods,” Polterovich mentioned.
“Attempting to show a long-standing conjecture is a sport. Discovering a chic answer is an artwork. And in lots of circumstances stunning mathematical discoveries do turn into helpful—you simply have to seek out the correct software.”
Reference: “Pólya’s conjecture for Euclidean balls” by Nikolay Filonov, Michael Levitin, Iosif Polterovich and David A. Sher, 5 June 2023, Inventiones mathematicae.
DOI: 10.1007/s00222-023-01198-1